搜狐创始人《张朝阳的物理课》推导麦克斯韦速度分布律！

12 时，《张朝阳的物理课》第二十九期准时开播。搜狐创始人、董事局主席兼 CEO 张朝阳坐镇搜狐视频直播间，探究玻尔兹曼分布，并以重力场和速度场为例进行讲解。

通过建立空气密度、重力、温度、压差之间的关系，推导得到空气粒子数密度随重力势能的分布；利用速度各分量的独立性、各向同性、理想气体状态方程等，推导得到麦克斯韦速度分布律，体现粒子数密度随动能的分布。两者均符合玻尔兹曼分布。这些也为解释大气中氢气含量之低提供了一个物理的视角。

“我们花了很长时间，研究量子力学和它的典型应用。先是氢原子能级，后来是双原子分子。”张朝阳开场直奔主题，“今天要研究玻尔兹曼在重力场和速度场的分布。“

玻尔兹曼分布：高处空气更稀薄？ 微分方程来建模

上节课，张朝阳利用玻尔兹曼分布，解释温度很低时自由度会被冻结，导致能量均分定理失效，最终得出比热容随温度的阶梯图。同时，计算粒子平均振动能以及普朗克黑体辐射时，也都用到了玻尔兹曼分布，足见其重要性与普遍性。今天，他想通过两个关于理想气体分布的具体计算实例，来直观呈现玻尔兹曼分布。

“先来看看简单的例子。”张朝阳尝试计算粒子质量为 m，温度为 T 的理想气体，在重力加速度为 g 的重力场下，其数密度 n 随高度 h 的变化。

他介绍说，在高度为 h 的地方，取一个底面积为 A，高度为 dh 的小层，则这层的体积为 Adh，一共有 nAdh 个粒子，每个粒子受向下的重力 mg，则这层气体受到的向下的重力为 mgnAdh。另外这层气体还受到上下两部分气体的压力，设上部分气体的压强为 p+dp，下部分气体的压强为 p，那么气体受到向上的推力为 Ap-A（p+dp）=-Adp，它必须与向下的重力 mgnAdh 相等才可以让这层气体受力平衡：

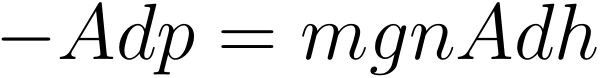
另外，将理想气体状态方程 p=nkT 代入上式，然后消掉两边的 A，并将右边的 n 移到左边后两边进行积分，最终得到气体数密度关于高度的分布：

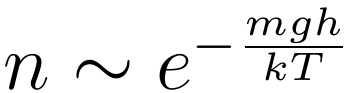
mgh 正是气体在重力场下的势能。可见大气中的粒子数密度符合玻尔兹曼分布。

麦克斯韦速度分布：各向同性定形式 总数和压强做归一

张朝阳还举了另外一个例子。同样也是理想气体，但此气体没有重力场等外场势能，只研究其中粒子在温度为 T 时的速度分布，该分布正是麦克斯韦速度分布。他边列公式边介绍，设一个微小的速度区内的粒子数密度为：

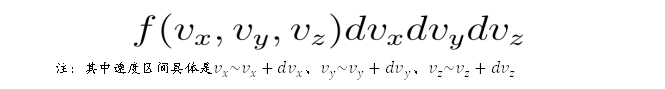
由于理想气体中的粒子是各向同性的，所以粒子数密度的分布 f 与粒子速度的方向无关，只与速度的大小有关。他在小白板上写下：

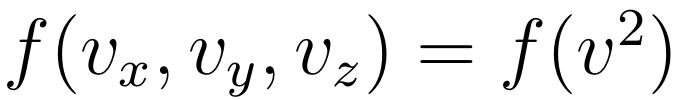
他解释，“我们还知道，理想气体中粒子之间无势能，而关于它们的碰撞也可以分解为相互独立的三个分量，所以粒子在三个方向上的速度分布是相互独立的，于是又可以将 f 写成如下形式。”

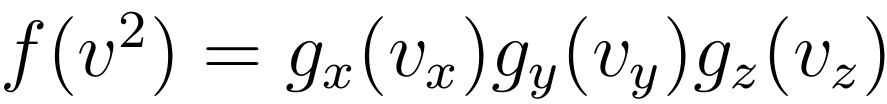
将上式等号两边取对数，可以将右边乘法变成加法，然后求其关于速度 x 分量的偏导，可得：

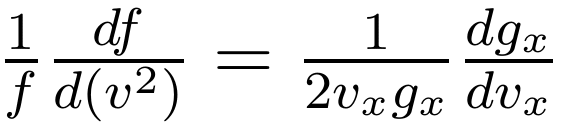
同理，对速度 y 与 z 分量求偏导也得到上式等号左边的量，结合起来就得到：

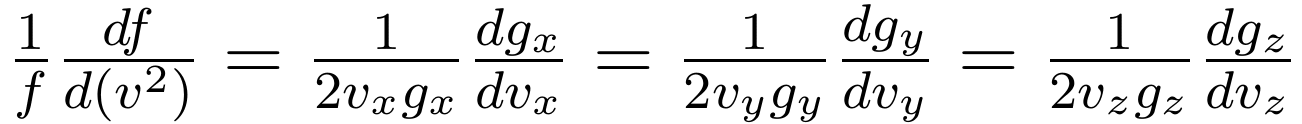
由于知道 g 函数只与对应的速度分量有关，而速度分量之间又是彼此独立的，那么上式只能等于一个与速度分量都无关的常数：

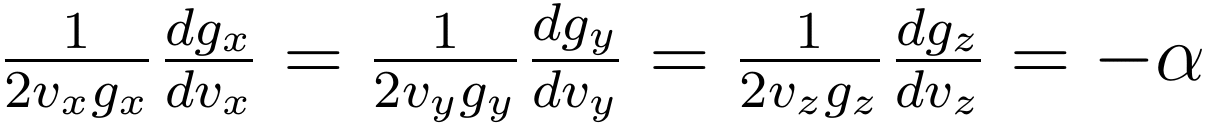
容易解得 g 函数：

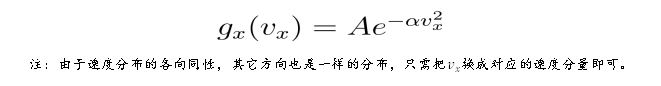
将 g 函数带回 f 的表达式，最终可以得到粒子数密度关于总速度的分布：

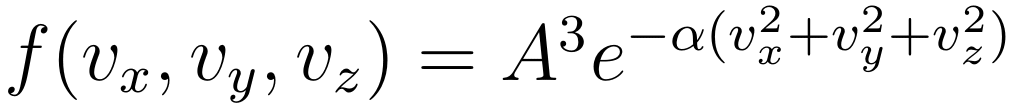
▲ 利用粒子速度分布的各向同性与三个方向分量的独立性推导麦克斯韦速度分布律

“接下来，我们还需要计算积分常数 A 以及参数 α。”他继续推导，将所有速度区间的粒子数密度加起来，可以得到理想气体的总粒子数密度 n：

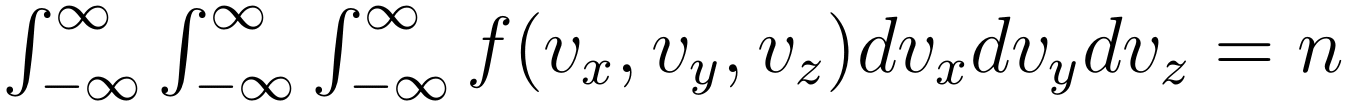
由此，可以计算得到 A 的具体表达式：

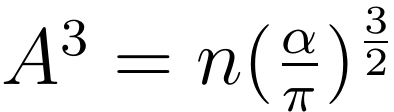
至于参数 α，则需要使用理想气体状态方程 p=nkT 来处理，张朝阳利用粒子对 zy 平面的容器壁的碰撞来计算压强 p。将其它速度其它分量积分可以得到速度 x 分量的分布：

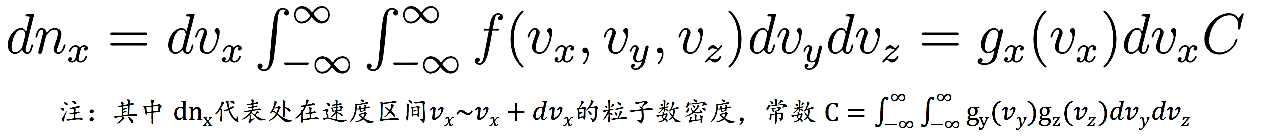
每个粒子碰撞容器壁后，x 方向上的动量大小相等方向反向，改变量为原动量 x 分量的 2 倍大小。计算所有向 x 正方向碰撞容器壁产生的压强：

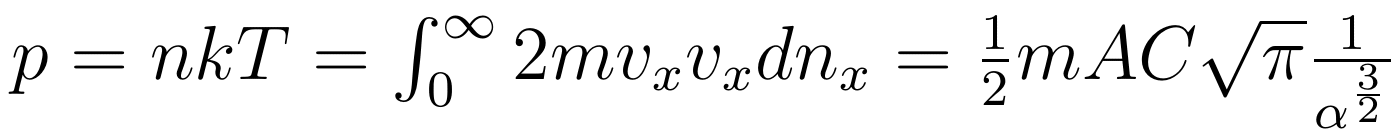
为了继续化简，将总粒子数密度 n 表达为 x 方向上的积分：

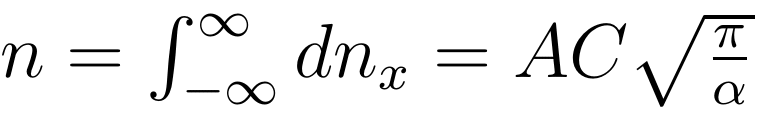
将此表达式代入 p=nkT 中，化简便可得到 α 的表达式：

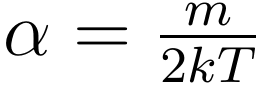
将 A 与 α 代回 f，最终得到麦克斯韦速度分布的表达式：

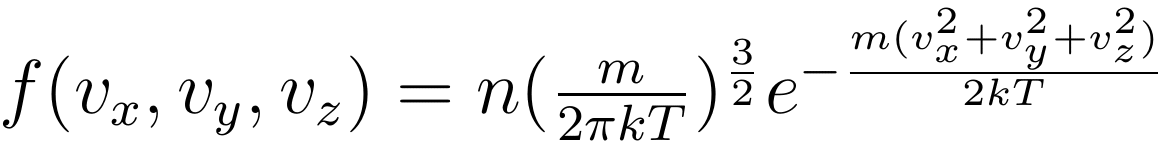
若进一步化为关于速度大小的表达式，则如下图所示：

▲ 张朝阳推导得到麦克斯韦速度分布

氢气在大气中为何少？ 利用麦克斯韦速度分布律推导解释

观察麦克斯韦速度分布公式，注意到 e 指数上除 kT 之外就是粒子的动能，这说明此分布也满足玻尔兹曼分布，张朝阳从物理学的角度，利用麦克斯韦速度分布解释了氢气为何在大气中那么少。

根据前面计算的粒子数密度关于高度的分布，由于氢气分子质量相比空气中其它分子的质量要小得多，所以其粒子数密度随高度衰减得没那么快，从而氢气可以爬得更高，再根据麦克斯韦速度分布律公式，氢气分子质量小还会导致它在速度较大的情况下仍有可观的分布，部分粒子的速度，可以超过第一宇宙速度甚至第二宇宙速度，从而逐渐逃逸，离开地球。这样氢气在大气中的含量就非常少了。

当然，这只是看待该问题的一个角度。实际上，从化学上讲，氢较为活泼，容易形成水等许多化合物，从而以其它形式相对固定地存在于地球上，也减少了它以单质形式存在于大气中的量。实际上，用原子质量较小但化学上更惰性的氦气作为例子，可以更好地体现这一物理规律的影响。

可以看到，在本节课中的两个例子都符合玻尔兹曼分布，其中一个 e 指数上的能量是粒子的势能，而另一个则是粒子的动能，可见玻尔兹曼具有普适性，下节课将具体讲解如何导出玻尔兹曼分布。直播结尾，张朝阳总结课程内容，“这是能量差和 kT 的战争。”