二维傅里叶变换是怎么进行的?
1.首先回顾一下一维FT
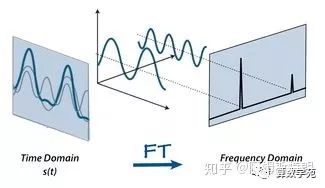
通俗来讲,一维傅里叶变换是将一个一维的信号分解成若干个三角波。
对于一个三角波而言,需要三个参数来确定它:频率,幅度 A ,相位。因此在频域中,一维坐标代表频率,而每个坐标对应的函数值也就是是一个复数,其中它的幅度就是这个频率三角波的幅度 A ,相位就是 。下图右侧展现的只是幅度图,在信号处理中用到更多的也是幅度图。
2.类比:从一维到二维
一维信号是一个序列,FT将其分解成若干个一维的简单函数(三角波)之和。二维的信号可以说是一个图片,类比一维,那二维FT是不是将一个图片分解成若干个简单的图片呢?
确实是这样,二维FT将一个图像分解成若干个三角平面波之和。如下图:
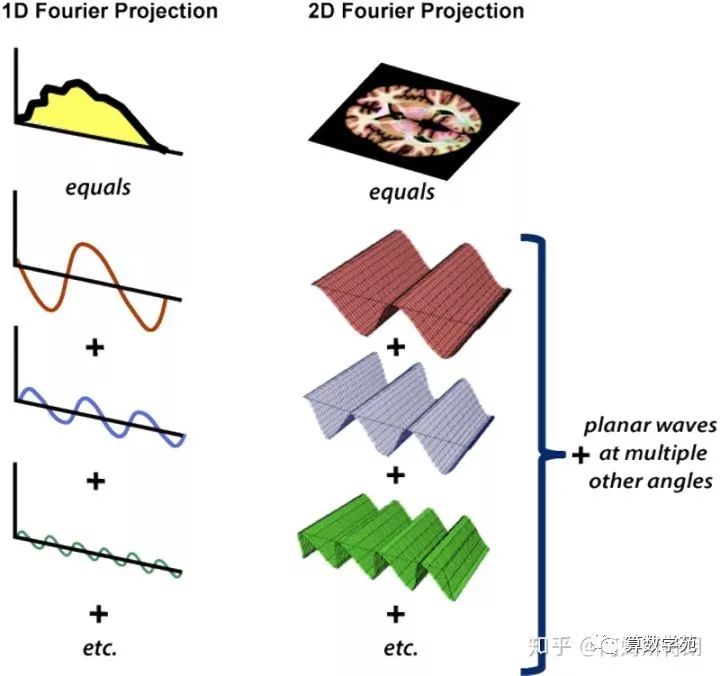
对于三角平面波,可以这样理解,在一个方向上存在一个三角函数,在法线方向上将其拉伸。前面说过三个参数可以确定一个一维的三角波。哪几个参数可以确定一个二维的三角平面波呢?答案是四个,其中三个和一维的情况一样(频率 ,幅度 A ,相位 ),但是具有相同这些参数的平面波却可以有不同的方向。如下图所示:
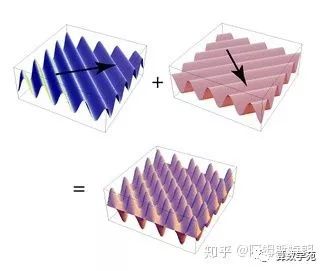
两个不同方向的平面波叠加
3.二维频率域K-SPACE
在一维中由于分解后的参数只要三个,所以用一个序列就能存储它:下标表示频率,存储的内容表示此频率的三角波的幅度和相位。而对于二维FT变换后的平面波有四个参数,那怎末来保存呢?
类比一维中,幅度和相位可以用一个复数表示,它可以作为我们存储的内容。但是还有两个:一个频率一个方向。这时想到向量是有方向的,也是有长度的。所以我们用一个二维的矩阵的来保存分解之后得到的信息。这个矩阵就是K空间。(一般用k来表示空间频率,单位是1/m)
什么意思呢?就是说一个二维矩阵点代表这个平面波的法向量,这个向量的模代表这个平面波的频率 ,这个点里面保存的内容复数就是此平面波的幅度和相位。下面这个图很好的体现了这一点:
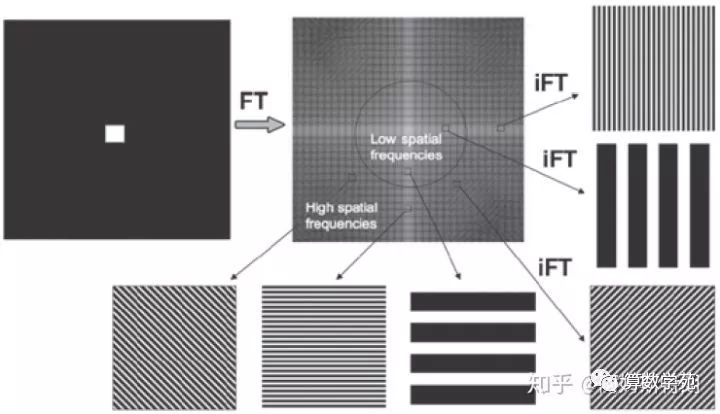
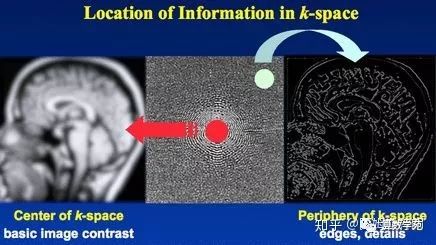
也因此K空间的中心对于低频,周围对于高频。如下图,K空间中只有(0,0)处有值,也就是信号都是直流即不存在变化,所以实空间就是一张白纸。

再如下面这个图片,中心低频贡献了图像的主体,周围高频提供图像的细节和边缘。
4.关于K空间
在一维FT变换后,频域呈现对称性,也就前半段代表(0,fs/2),而后半段代表(-fs/2,0)。在二维中也是如此。因此为了方便理解,一般会对图像进行fftshift,将其交叉替换,将0频移至中心。另外,K空间也具有共轭对称性。
下面这个图像显示了二维傅里叶变换中,实空间旋转多少,频率空间也会相应旋转多少。这其实是高维傅里叶变换缩放定理的一种特殊情况。

5.二维傅里叶变换公式
上式为二维FT的公式。可以证明的实部也就是是一个三角平面波。也就是说,二维FT的公式就是将与每个不同方向不同频率的平面波做积分,求出这个基的系数。至于为什么这样可以,就要涉及到正交基、内积、线性空间的知识了。
相关文章
-
李开复:未来几年,中国最赚钱的工作是什么?
文章来源:老铁商城2019-10-29 -
2019年全球十大突破性技术
文章来源:老铁商城2019-10-29 -
科学家为什么钟情艺术?因为数学和绘画、音乐有相似的美感
文章来源:老铁商城2019-10-20 -
价格上涨“劝退”用户,奈飞为何逆流而行?
文章来源:老铁商城2019-10-18 -
王思聪“股权遭冻结”又上热搜!王健林当初给的“练手资金”还好吗?
文章来源:老铁商城2019-10-18 -
滴滴宣布开放城市交通指数数据集 助力交通领域科研发展
文章来源:老铁商城2019-10-18 -
A16Z合伙人:那些“连错都谈不上”的技术预测
文章来源:老铁商城2019-10-18

 2019-10-21 23:22:38
2019-10-21 23:22:38




